6.2 Hypothesis Tests
6.2.1 Illustrating a Hypothesis Test
Let’s say we have a batch of chocolate bars, and we’re not sure if they are from Theo’s. What can the weight of these bars tell us about the probability that these are Theo’s chocolate?
set.seed(20)
choc.batch <- rnorm(20, mean = 42, sd = 2)
summary(choc.batch)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 36.22 40.81 41.41 41.62 42.87 45.57Now, let’s perform a hypothesis test on this chocolate of an unknown origin.
What is the probability of observing a mean of 41.62 under the hypothesis that these are Theo’s chocolate bars? We did not have an expectation that these would be heavier or lighter when we started, so this is a two-sided test, with:
Null hypothesis: \(H_0: \mu = 40\).
Alternative: \(H_A: \mu \neq 40\).
The theoretical distribution of the sample mean is: \(\bar{X} \sim {\cal N}(\mu, \sigma/\sqrt{n})\)
mu.0 <- 40
sigma.0 <- 2
n <- length(choc.batch)
x.bar <- mean(choc.batch)
curve(dnorm(x, mean = mu.0, sd = sigma.0/sqrt(n)), xlim = c(38, 42),
main = "Distribution of Chocolate Weight Under Null Hypothesis",
xlab = "Chocolate Bar Weight (in g)", ylab = "Density", col = "blue")
abline(v = mean(choc.batch), lwd = 2)
text("Unknown batch mean", x = mean(choc.batch), y = 0.6, cex = 0.8, pos = 2)
text("Sampling distribution", x = mu.0, y = 0.3, cex = 0.8, col = "blue")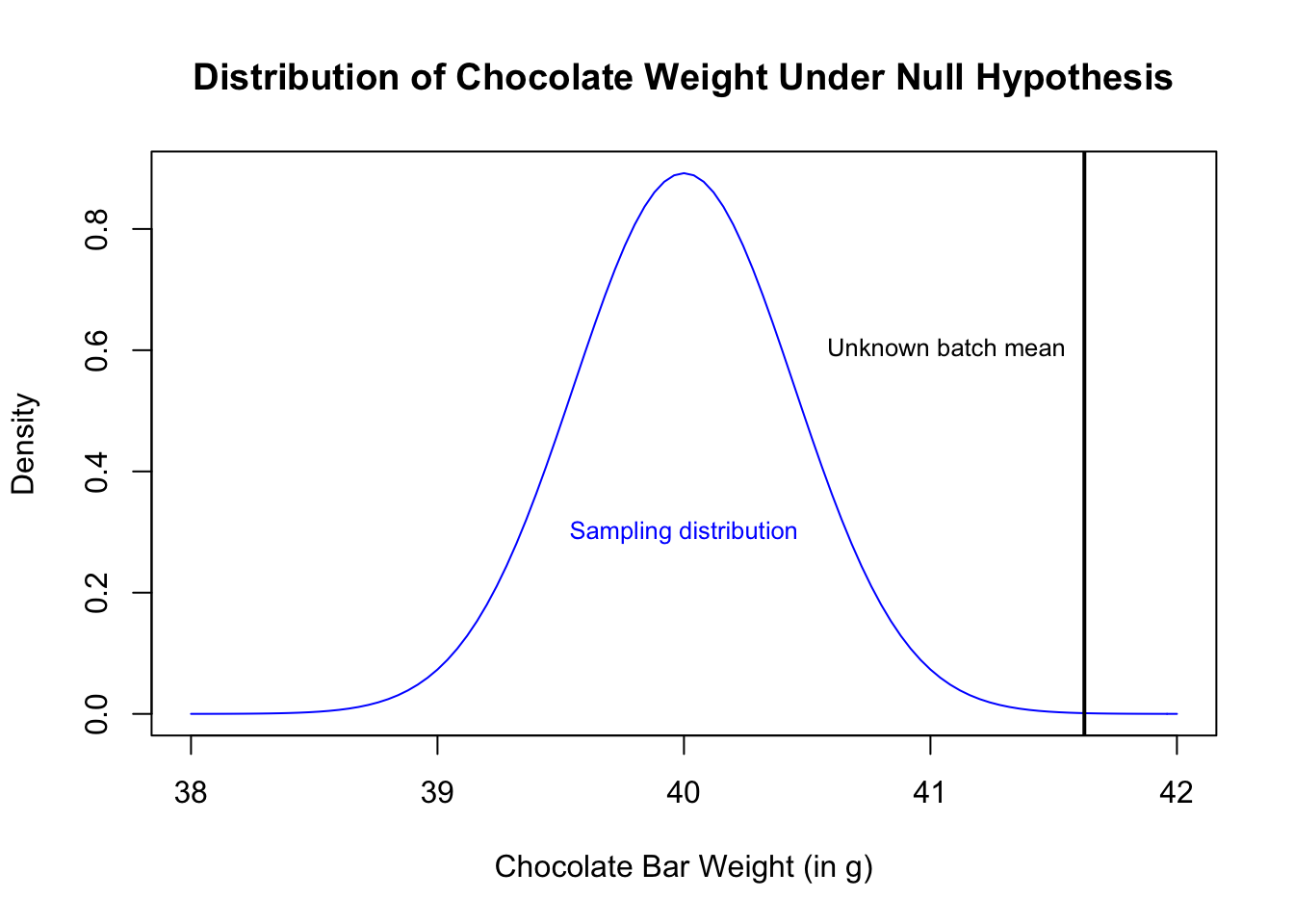
And the probability of this event, also called the two-sided p-value, is
(1 - pnorm(x.bar, mean = mu.0, sd = sigma.0/sqrt(n))) * 2## [1] 0.0002807644which is not very likely! So this chocolate is probably not from Theo’s.
6.2.2 Hypothesis Tests for Means
6.2.2.1 Known Standard Deviation
It is simple to calculate confidence intervals in R. If we know the population standard deviation, we typically use a hypothesis test based on the standard normal, called a Z-test. We can easily perform this test in R using the z.test() function from the BSDA package. We supply the hypothesized mean, the population standard deviation, and the level of the test like so,
library(BSDA)
z.test(x = choc.batch, mu = 40, sigma.x = 2, conf.level = 0.95)##
## One-sample z-Test
##
## data: choc.batch
## z = 3.6324, p-value = 0.0002808
## alternative hypothesis: true mean is not equal to 40
## 95 percent confidence interval:
## 40.74795 42.50099
## sample estimates:
## mean of x
## 41.62447z.test(x = choc.batch, mu = 40, sigma.x = 2, conf.level = 0.95)$p.value## [1] 0.00028076446.2.2.2 Unknown Standard Deviation
If we do not know the population standard deviation, we typically use the t.test() function included in R by default. We know that: \[\frac{\overline{X} - \mu}{\frac{s_x}{\sqrt{n}}} \sim t_{n-1}\] We supply the confidence level like so,
t.test(x = choc.batch, mu = 40, conf.level = 0.95)##
## One Sample t-test
##
## data: choc.batch
## t = 3.3849, df = 19, p-value = 0.003109
## alternative hypothesis: true mean is not equal to 40
## 95 percent confidence interval:
## 40.61998 42.62896
## sample estimates:
## mean of x
## 41.62447t.test(x = choc.batch, mu = 40, conf.level = 0.95)$p.value## [1] 0.003109143We note that the p-value here is 0.0031091, so again, we can detect it’s not likely that these bars are from Theo’s. Even with a very small sample the t-test is doing a good job.
6.2.3 Two-sample Tests
6.2.3.1 Unpooled Two-sample t-test
Now suppose we have two batches of chocolate bars, one of size 40 and one of size 45. We want to test whether they come from the same factory. However we have no information about the distributions of the chocolate bars. Therefore, we cannot conduct a one sample t-test like above as that would require some knowledge about \(\mu_0\), the population mean of chocolate bars.
We will generate the samples from normal distribution with mean 45 and 47 respectively. However, let’s assume we do not know this information. The population standard deviation of the distributions we are sampling from are both 2, but we will assume we do not know that either. Let us denote the unknown true population means by \(\mu_1\) and \(\mu_2\).
batch.1 <- rnorm(n = 40, mean = 45, sd = 2)
batch.2 <- rnorm(n = 45, mean = 47, sd = 2)
boxplot(batch.1, batch.2, border=c("blue","black"),
main="Boxplot for chocolate bars from two batches",
names=c("Batch 1","Batch 2"), ylab="Chocolate bar weight")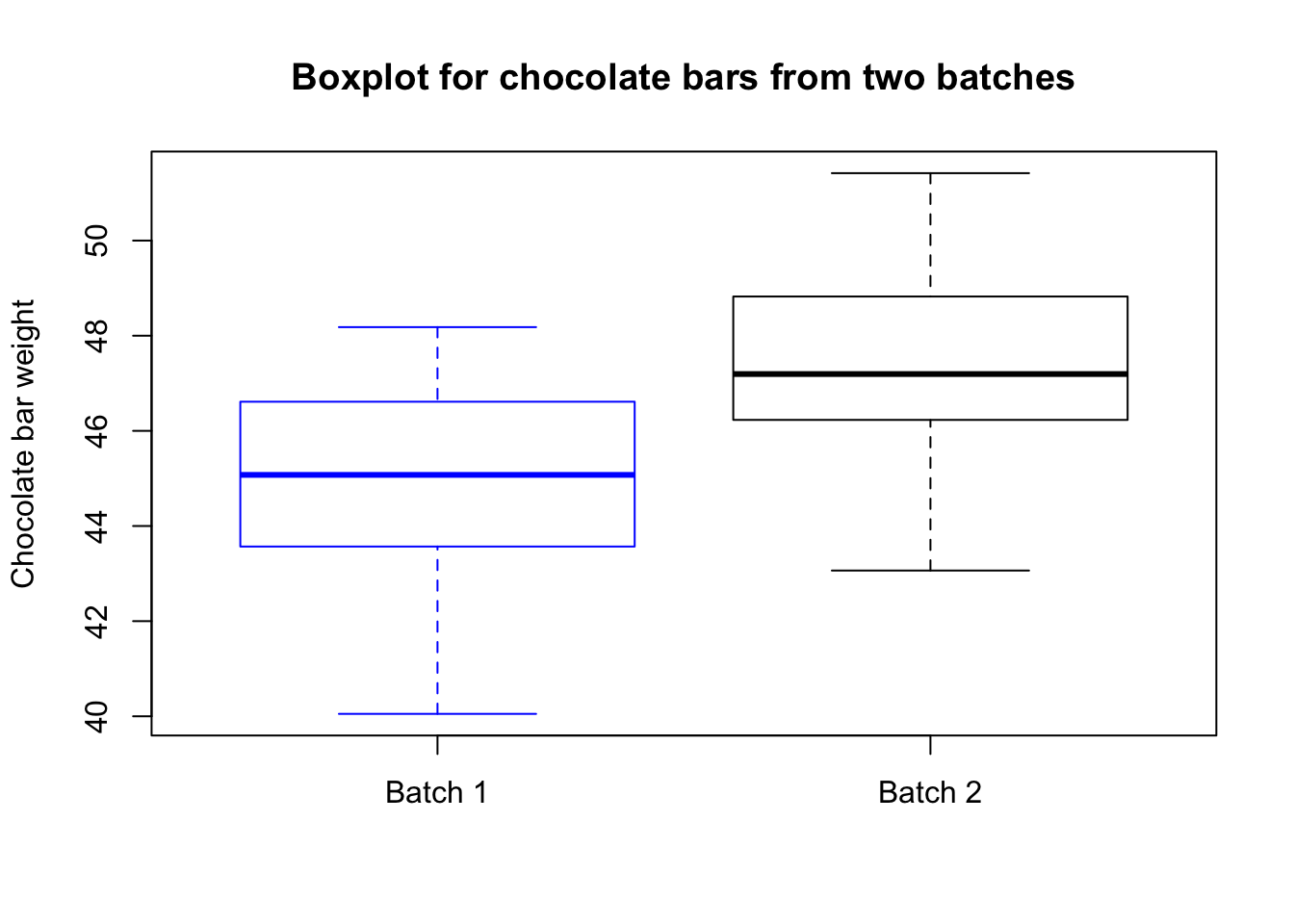
Consider we want to test \(H_0:\mu_1=\mu_2\) versus \(H_1:\mu_1\neq\mu_2\). We can use R function t.test again.
t.test(batch.1, batch.2)##
## Welch Two Sample t-test
##
## data: batch.1 and batch.2
## t = -5.658, df = 80.33, p-value = 2.278e-07
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -3.197527 -1.533586
## sample estimates:
## mean of x mean of y
## 44.98055 47.34611The p-value is less than .05, so we reject the test. Indeed, we know from simulating the data that \(\mu_1\neq\mu_2\).
Consider testing \(H_0:\mu_1=\mu_2\) versus \(H_1:\mu_1\leq\mu_2\).
t.test(batch.1, batch.2, alternative="less")##
## Welch Two Sample t-test
##
## data: batch.1 and batch.2
## t = -5.658, df = 80.33, p-value = 1.139e-07
## alternative hypothesis: true difference in means is less than 0
## 95 percent confidence interval:
## -Inf -1.669838
## sample estimates:
## mean of x mean of y
## 44.98055 47.34611As expected, this test is also rejected.
6.2.3.2 Pooled Two-sample t-test
Suppose you knew that the samples are coming from distributions with same standard deviations. Then it makes sense to carry out a pooled 2 sample t-test. You can use the following R command.
t.test(batch.1, batch.2, var.equal = TRUE)##
## Two Sample t-test
##
## data: batch.1 and batch.2
## t = -5.6794, df = 83, p-value = 1.941e-07
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -3.193986 -1.537127
## sample estimates:
## mean of x mean of y
## 44.98055 47.346116.2.3.3 Paired t-test
Suppose we take a batch of chocolate bars and stamp the Theo’s logo on them. We want to know if the stamping process changes the weight of the chocolate bars.
choc.after <- choc.batch + rnorm(n = 20, mean = -0.3, sd = 0.2)par(mfrow = c(1,2))
boxplot(choc.batch, choc.after, border=c("blue","black"),
main="Boxplot for before and after",
names=c("Before","After"), ylab="Chocolate bar weight")
boxplot(choc.after - choc.batch, main="Boxplot for weight difference")
abline(h = 0, lty = 3, col = rgb(0, 0, 0, 0.5))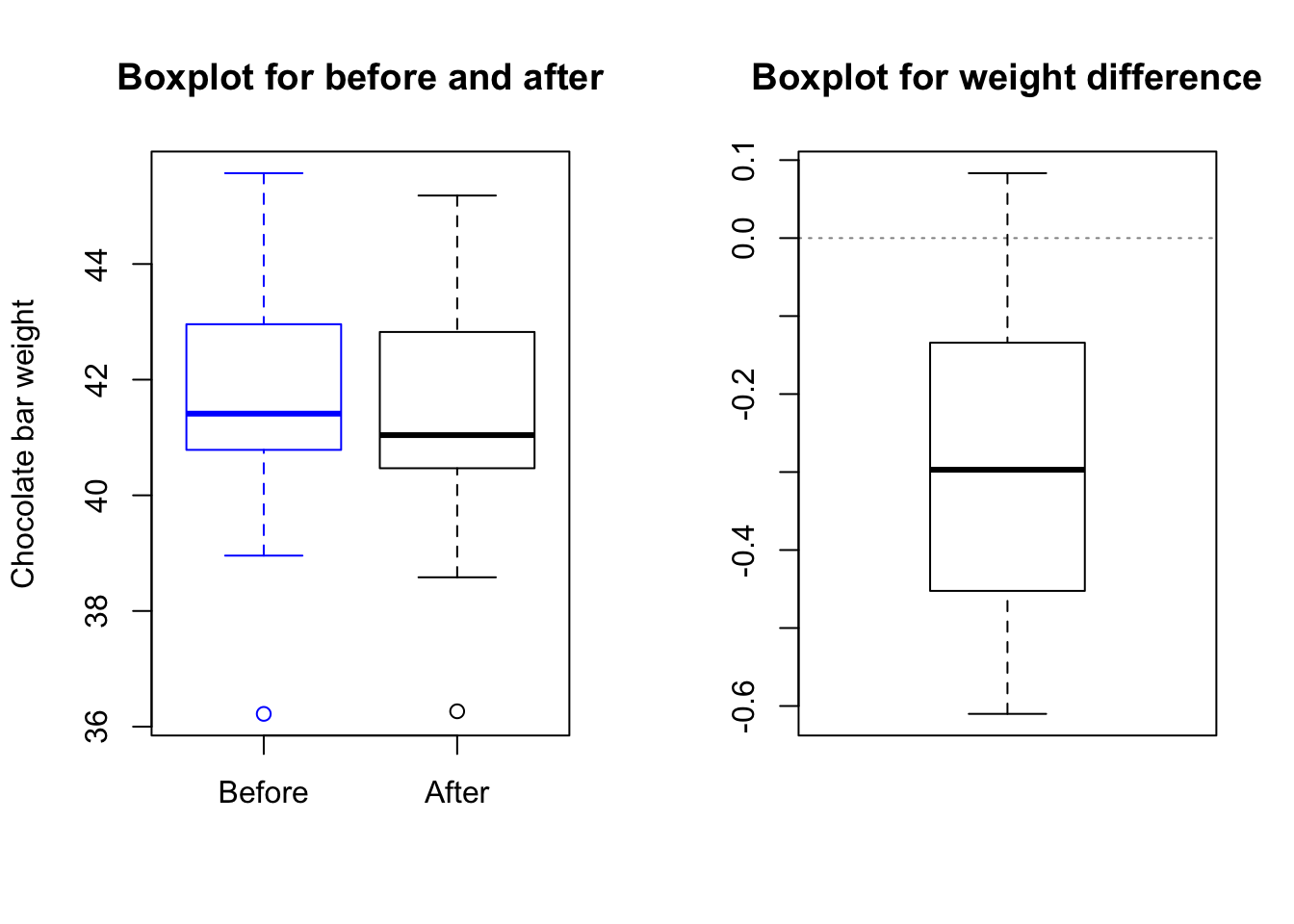
Let \(\mu_1\) and \(\mu_2\) be the true means of the distributions of chocolate weights before and after the stamping process. Suppose we want to test \(H_0:\mu_1=\mu_2\) versus \(\mu_1\neq\mu_2\). We can use R function t.test() for this by choosing paired = TRUE.
t.test(choc.after, choc.batch, paired = TRUE)##
## Paired t-test
##
## data: choc.after and choc.batch
## t = -5.9034, df = 19, p-value = 1.103e-05
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -0.3838959 -0.1829305
## sample estimates:
## mean of the differences
## -0.2834132We can also perform the same test as a one sample t-test using choc.after - choc.batch.
t.test(choc.after - choc.batch)##
## One Sample t-test
##
## data: choc.after - choc.batch
## t = -5.9034, df = 19, p-value = 1.103e-05
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## -0.3838959 -0.1829305
## sample estimates:
## mean of x
## -0.2834132Notice that we get the exact same p-value. It proves that we had the same test.
Since the p-value is less than .05, it indicates that the test will be rejected at level .05. Hence, we have enough evidence in the data to claim that stamping a chocolate bar reduces its weight.
6.2.4 Tests for Proportions
Let’s look at the proportion of Theo’s chocolate bars with a weight exceeding 38g:
table(choc > 38) / length(choc)##
## FALSE TRUE
## 0.1607 0.8393Going back to that first batch of 20 chocolate bars of unknown origin, let’s see if we can test whether they’re from Theo’s based on the proportion weighing > 38g.
table(choc.batch > 38) / length(choc.batch)##
## FALSE TRUE
## 0.05 0.95count.unknown <- sum(choc.batch > 38)
count.unknown## [1] 19Recall from our test on the means that we rejected the null hypothesis that the means from the two batches were equal. In this case a one-sided test is appropiate and our hypothesis is:
Null hypothesis: \(H_0: p = 0.85\).
Alternative: \(H_A: p > 0.85\).
We want to test this hypothesis at a level \(\alpha = 0.05\).
In R, there is a function called prop.test() that you can use to perform tests for proportions. Note that prop.test() only gives you an approximate result.
prop.test(count.unknown, length(choc.batch), p = 0.85, alternative = "greater")## Warning in prop.test(count.unknown, length(choc.batch), p = 0.85,
## alternative = "greater"): Chi-squared approximation may be incorrect##
## 1-sample proportions test with continuity correction
##
## data: count.unknown out of length(choc.batch), null probability 0.85
## X-squared = 0.88235, df = 1, p-value = 0.1738
## alternative hypothesis: true p is greater than 0.85
## 95 percent confidence interval:
## 0.7702849 1.0000000
## sample estimates:
## p
## 0.95Similarly, you can use the binom.test() function for an exact result.
binom.test(count.unknown, length(choc.batch), p = 0.85, alternative = "greater")##
## Exact binomial test
##
## data: count.unknown and length(choc.batch)
## number of successes = 19, number of trials = 20, p-value = 0.1756
## alternative hypothesis: true probability of success is greater than 0.85
## 95 percent confidence interval:
## 0.7838938 1.0000000
## sample estimates:
## probability of success
## 0.95The p-value for both tests is around 0.1755579, much higher than 0.05. So in this case we cannot reject the hypothesis that the unknown bars come from Theo’s. This is not because the tests are less accurate than the ones we ran before, but because we are testing a less sensitive measure: the proportion weighing > 38 grams, rather than the mean weights.
The prop.test() function is the more versatile function in that it can deal with contingency tables, larger number of groups, etc. The binom.test() function gives you exact results, but you can only apply it to one-sample questions.
6.2.5 Power
Let’s think about when we reject the null hypothesis. We would reject the null hypothesis if we observe data with too small of a p-value. We can calculate the critical value where we would reject the null if we observe data more extreme than that.
Suppose we take a sample of chocolate bars of size n = 20, and our null hypothesis is that the bars come from Theo’s (\(H_0\): mean = 40, sd = 2). Then for a one-sided test (versus larger alternatives), we can calculate the critical value with
mu0 <- 40
alpha <- 0.05
n <- 20
stddev <- 2
crit <- qnorm(1 - alpha, mean = mu0, sd = stddev / sqrt(n))
crit## [1] 40.7356Now suppose we want to calculate our chances of rejecting the null hypothesis when the null hypothesis is false. In order to do so, we need to compare the null to a specific alternative, so we choose \(H_a\): mean = 42, sd = 2. Then the probability that we reject the null under this specific alternative is
mua <- 42
1 - pnorm(crit, mean = mua, sd = stddev / sqrt(n))## [1] 0.9976528We can use R to perform the same calculations using the power.z.test from the asbio package.
asbio::power.z.test(n = n, effect = mua - mu0, sigma = stddev,
alpha = alpha, test = "one.tail")$power## [1] 0.9976528